I support legal heavy pi!
While we're on the subject of abstract mathy stuffs, this is a good a time as any to bring up this idea that came up the other day... I'm pretty confident I didn't invent any new calculus, but my professor (who isn't a PhD, for whatever that's worth) couldn't come up with an answer for me when I asked him about it. Either it exists and has next to no use, or more likely I made some assumption somewhere that doesn't work.
Essentially it deals with derivatives of equations with base 'e', which have a rather unique property in that the function and its derivative are the same when it's simply f(x) = e^x.
My logic seems to result in a simple formula not only for the first, second, or third derivative of an equally simple formula, as well as a slightly more complicated e^(nx) where n is some constant, such as 3 in the example below... but it seems to devolve into crazyland when it seems to work to find (in addition to those first, second, and third derivatives) the one and a halfth© derivative, three and three quartersth© derivative, pi'th© derivative, and so on.
Apologies for those not using Glade theme! I was afraid to use transparent background for fear of black text on potential black backgrounds!
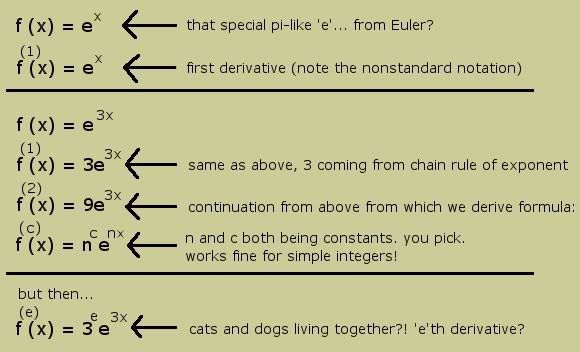
My brain can't make heads or tails of what it would mean, but it seems to work.

There are other things in mathematics that my brain can't wrap itself around anyway, so that's hardly a damning quality. Even simple calculators don't balk at 3 to the 1.5th power, but that has to be kinda mind-blowing to someone thinking exponents means to multiply the base by itself that many times. I've done a little searching about for something along the lines of "non-integer order derivatives" and the like but haven't come up with anything relevant beyond some programmer coming to a similar conclusion as an afterthought... and that's hardly a quality source!
So... do I get any clever points for stumbling upon existing math or did I just make a dumb assumption somewhere? :p When I was typing up the graphic I am feeling less than secure about my n^c part of it (as per above paragraph), but I can't say I am too fresh in my math basics. It's been 10 years since I had a calculus class and 8 since I've had a math class of any kind.



