None of this is going to answer your Einstein thought-experiment, but it's relevant to the discussion at hand. I'm not going to touch on Doppler shifting, because that's based on waves being emitted by a moving source. Doppler shift causes frequencies and wavelengths to be measured differently from their actual values. You can read about it here:
http://en.wikipedia.org/wiki/Doppler_shiftThere are currently theories being put forth that the value of certain scientific constants have changed over the history of the universe. For example G, or the gravitation constant, has not always been equal to

. If that were the case, even for just that one number, it would have wide-ranging implications on physical law. Proponents claim that it is true for many more constants.
The problem with such a theory is that those numbers were obtained through experimentation, and often with instruments that are nowhere near as precise as what we have today. They are also, by their very nature, approximations. It would be very difficult (not impossible, just difficult) to prove that they are changing.
The speed of light is given by the following equation: c = 1/√(ε0μ0)
ε0 is the electrical permittivity constant of a vacuum
μ0 is the magnetic permeability constant of a vacuum
We may extend this further to state that, for any medium, c = 1/√(εμ) where ε and μ are the permittivity and permeability constants associated with that medium. As such, the speed of light that we are all familiar with (3x10^8) is more correctly written as c0 - the speed of light in a vacuum.
That we can relate the speed of light to electric and magnetic constants makes sense when you stop to consider what light is - an electromagnetic wave. You may have covered sound in physics, and discussed how the velocity of a sound wave is the product of its frequency and wavelength. This is the same for electromagnetic waves, except they always have a speed of 1/√(εμ). Most of space is a vacuum, which gives us the c we all know and love.
The speed of light could change, but doing so would also require that the electrical permittivity and magnetic permeability of a vacuum changes to go along with it. As I mentioned above, it's been theorized that some scientific constants have actually changed, and there are claims to have supporting evidence. Those are two of the big ones.
This still doesn't mean that you can travel faster than the speed of light. Much of that revolves around the metric for measuring space. You are familiar with the Pythagorean theorem. It leads to the distance formula that your algebra teacher made you memorize.

With a little work, we can also find the hypotenuse of a triangle that lies in x-y-z coordinate space, rather than just in an x-y plane. This leads to the following as the distance formula in 3-space
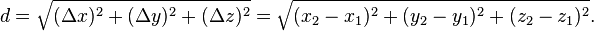
We can take this a step further, and use that formula to find the length of curvy lines - things that can't be turned into a right triangle. First, I will replace the left side of the equation with S. (Reason being, I'm about to start using the lower-case d for something else). I now have:
S^2 = x^2 + y^2 + z^2
It can also be written as
S = √(x^2 + y^2 + z^2)
With this formula, I'm still only able to use straight lines. I can't find the length of wiggly lines without calculus. To do that, I have to chop my curve S up into lots of little tiny pieces, dS. Each little piece dS is so tiny that it's close to being straight. The more pieces I chop S into, the closer each dS gets to being straight. If I use an infinite number of dS pieces, they will all be straight. Anyone who has had basic calculus would recognize this as leading up to a Riemann sum, only I'm not using rectangles to approximate area, I'm using tiny slices of length to approximate arc length. This leads to the following formula:
dS = √(dx^2 + dy^2 + dz^2)
If I then write S as a parametric curve, meaning I write x, y, and z as functions of another variable (usually t), I have the following:
dS = √[(dx/dt)^2 + (dy/dt)^2 + (dz/dt)^2]dt
What I'm doing is adding up little bits and pieces of S, which I find by adding together the squares of the coordinate components of its first time-derivative. It's a formula that's very familiar to any student that's taken multivariable calculus. I end up with this:
S = ∫√[(dx/dt)^2 + (dy/dt)^2 + (dz/dt)^2]dt a<t<b
That may be a little confusing to read. Here is an image that makes it look a little more like you'd see in a textbook.

That's what it looks like for two dimensions. Just imagine a third term under there, only with z.
This integral concept is very important. If you've never taken calculus, don't worry quite so much about how to actually take an integral. Just understand that I'm adding up a lot of little tiny pieces to get something large.
Now, you should have noticed a pattern emerging when I was writing out the distance formulas for two and three dimensions. If I had a fourth dimension, you might think that the distance formula looks something like this:
S^2 = w^2 x^2 + y^2 + z^2
That is a valid metric for four-dimensional geometry. You've probably heard time listed as the fourth dimension, which would lead you to assume that the metric for four-dimensional space-time looks like this:
S^2 = x^2 + y^2 + z^2 + t^2
You would be wrong. For starters, the units aren't right. x, y, and z are all spatial dimensions, while t is a time dimension. That's easily fixed by multiplying t by a velocity (specifically: light in a vacuum), giving us the following:
S^2 = x^2 + y^2 + z^2 + (c*t)^2
You would still be wrong. According to Einstein's theory of special relativity, the metric for real four-dimensional space-time is actually:
S^2 = x^2 + y^2 + z^2 - (c*t)^2
What's the difference? Look closer. There is a subtraction symbol in front of the t term! Now, even this metric isn't entirely correct, because it doesn't account for the curvature of space-time due to a large concentration of mass. That's general relativity, and we aren't going there.
If I attempt to find arc length in a four-dimensional space-time, I would use a formula that looks like:
dS^2 = dx^2 + dy^2 + dz^2 - c^2*dt^2
I would parameterize that curve with some letter that isn't t (u and v are good choices, or perhaps the Greek letter tau), and then integrate with respect to my parameter.
Going back to that negative sign in the metric of four-dimensional space-time, for a moment. It seems like such a small, tiny little thing. That little change in arithmetic is the difference between a universe where faster-than-light travel is possible, and one where it isn't. (The reason why isn't something I've taken the time to explore, so I'm unable to elaborate further). This is where the concept of imaginary time comes from. Physicists often use the transformation t->
it, so that when the time term is squared,
i is squared along with it, comes out to be -1, and changes the sign on the time term.
I also want to take a moment to revisit that equation in its entirety.
dS^2 = dx^2 + dy^2 + dz^2 - c^2*dt^2
There is a very profound difference between the two sides of that equation. One side, the left, is a real thing. It exists. You can see it with your own eyes. You can measure it with a ruler. The right side of that equation is a mathematical construct. We use it to help us understand and study the universe. It's a tool. It's accurate, but it's just a tool. It's held up to scrutiny, however, unlike the previous metric where we had addition all the way across.
At any rate even if the value for the speed of light in a vacuum were to change, it would also change in the metric for measuring space-time. We would still find it impossible to travel faster than light.



